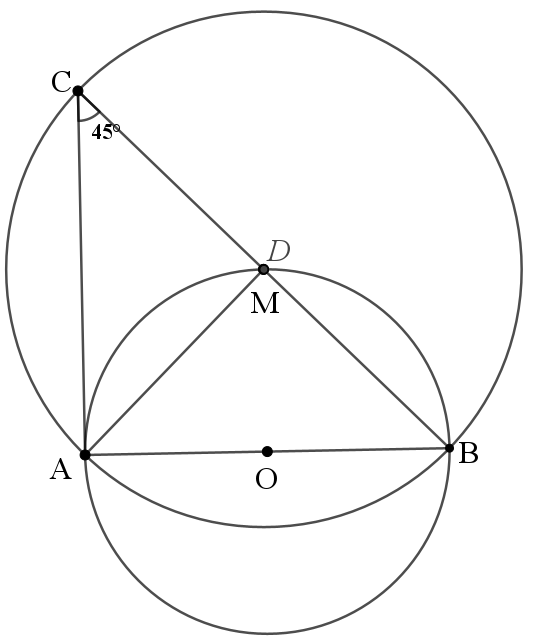
圆直径为6,M为圆弧上一动点,求AM+BM的最大值
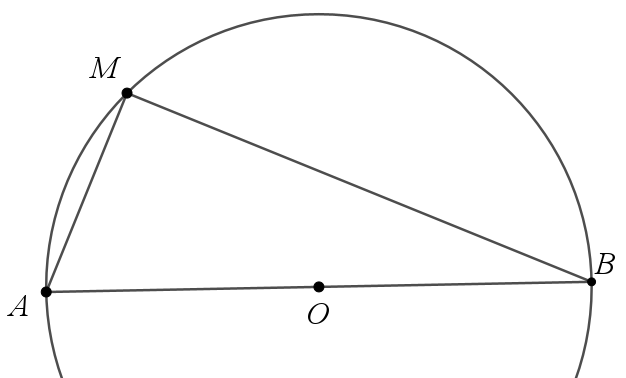
解:代数法:
设△ABM的面积为S,得,AM×MB=2S,
要求AM+BM的最大值,
可求的最大值。
即,
显然只要S大,AM+BM就最大。
△ABM,AB为定长,只要高最大△ABM面积就最大,
当点M运动到点O最上方时,高最大,为半径3,
所以,此时有,
![]()
则,AM+BM最大为![]() 。
。
几何法:
AM绕点M顺时针旋转90°,
则∠ACM=45°
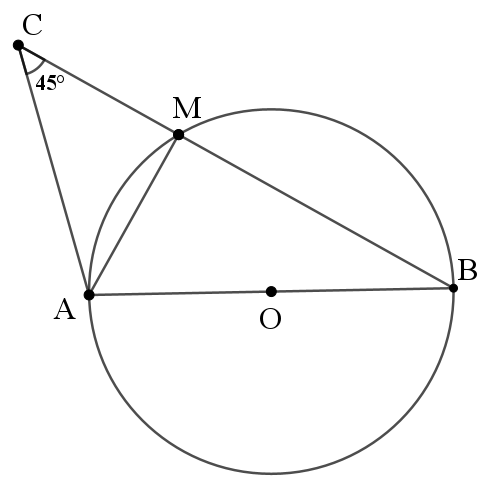
AB=6, ∠ACM=45°,定弦定角
点C在以点D为圆心的圆上运动。
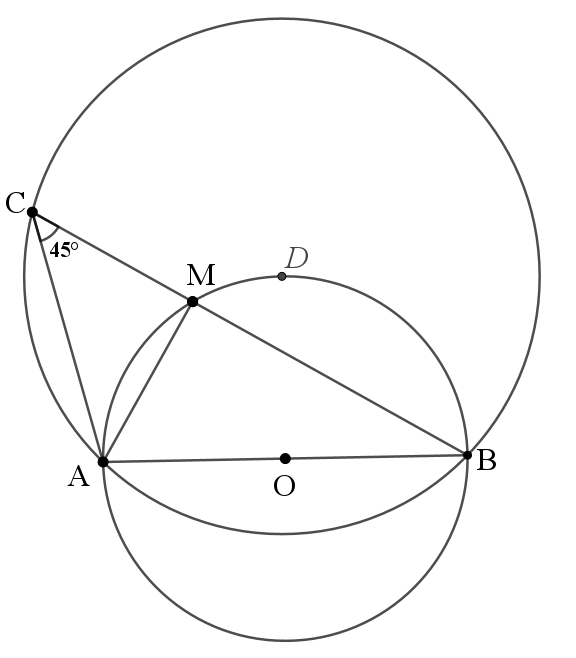
要求AM+BM最大,就是求BC最大。
当弦BC为直径时最大,D,M重合。
此时,△ABM为等腰直角三角形
则,![]() ,
,
AM+BM最大为 ![]() 。
。