如图,边长为2的正方形ABCD中,E、F分别为BC、CD上的动点,BE=CF,连接AE、BF交于点P,
则![]() 的最小值为?
的最小值为?
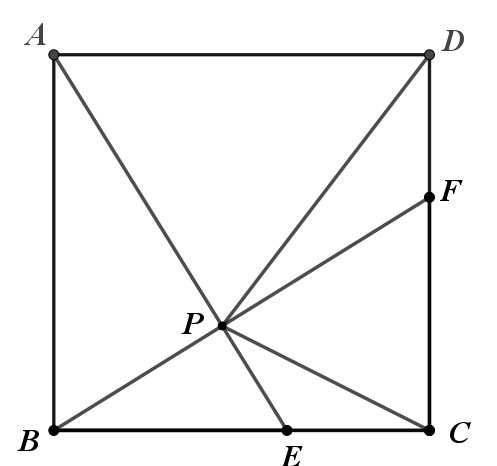
解:十字架模型:△BCF≌△ABE,得∠APB=90°
隐圆:AB定长为2,∠APB=90°,定长定角,点P的轨迹是圆
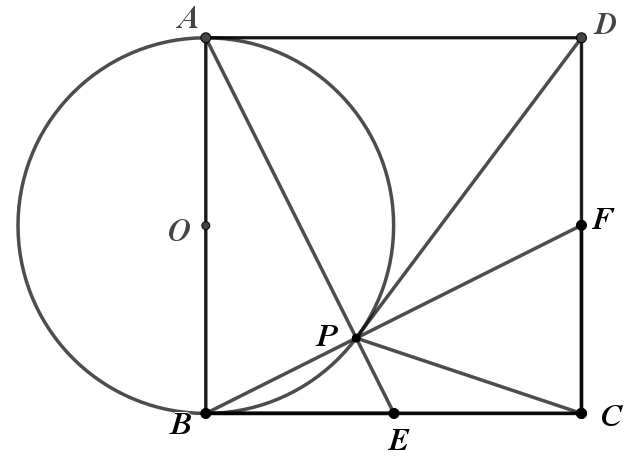
确定阿氏圆:![]() ,
,![]() 中 , 容易得出,
中 , 容易得出,![]() ,
,
构造相似:在OP上截取OK,使得 ,![]()
则△OPK∽△OCP。
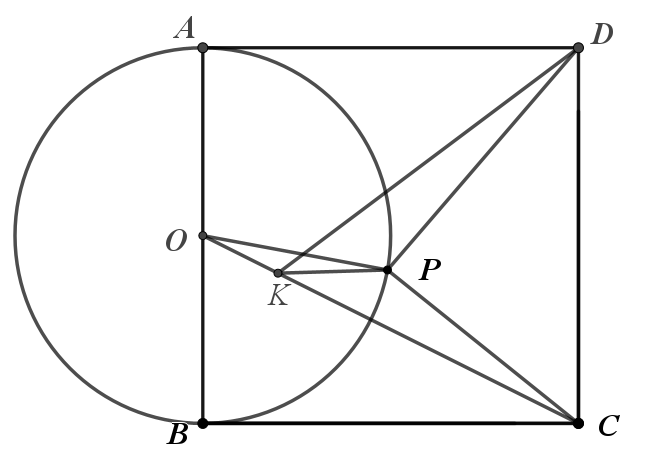
最小值:△OPK∽△OCP,![]() , 即求PD+PK最小
, 即求PD+PK最小
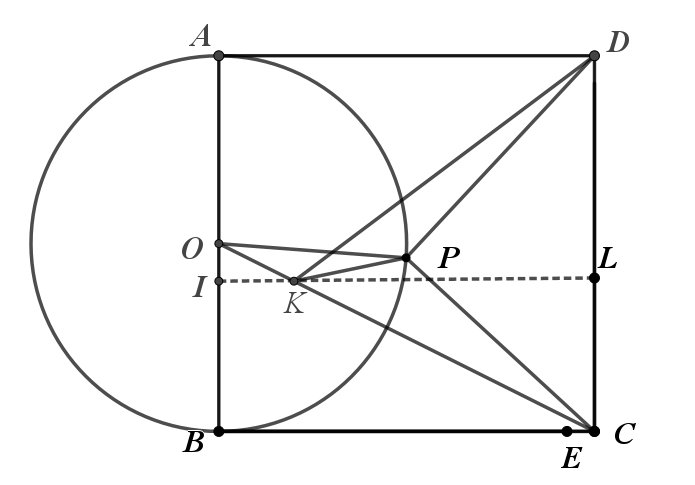
两点之间线段最短:连接DK ,即求DK
求值:作IL⊥CD,由勾股定理、相似求得,DK=2
如图,边长为2的正方形ABCD中,E、F分别为BC、CD上的动点,BE=CF,连接AE、BF交于点P,
则![]() 的最小值为?
的最小值为?

解:十字架模型:△BCF≌△ABE,得∠APB=90°
隐圆:AB定长为2,∠APB=90°,定长定角,点P的轨迹是圆

确定阿氏圆:![]() ,
,![]() 中 , 容易得出,
中 , 容易得出,![]() ,
,
构造相似:在OP上截取OK,使得 ,![]()
则△OPK∽△OCP。

最小值:△OPK∽△OCP,![]() , 即求PD+PK最小
, 即求PD+PK最小
两点之间线段最短:连接DK ,即求DK
求值:作IL⊥CD,由勾股定理、相似求得,DK=2
