在这一内容复习里，除了要了解基本题型，掌握基本知识点外，应该弄清楚考察次数较多，考察难度较大的知识点。下面我们来看看这一内容的考察难点：
第一讲：实数
难点1 绝对值
绝对值的定义：数轴上表示数的点到原点的距离，比如-3到原点的距离为3，我们就称-3的绝对值为3，记作|-3|=3，另外要知道正数，负数，0的绝对值分别是什么。其实定义已经很明确的告诉我们，正数的绝对值就是它本身，比如3，按照定义3到0的距离为3，所以|3|=3；负数的绝对值是它的相反数，比如刚才举例的-3；0的绝对值是0.
学生容易理解：学生总是认为任何一个数的绝对值是正数，比如|5|=5，当求数的绝对值这么认为还好，但是当求字母b的绝对值，也会直接认为|b|=b，容易忘记b的符号，这部分学生总是觉得不带负号就是正数，所以没有考虑字母的负号。
正确理解：求绝对值时，一定先要考虑绝对值负号里面的任意一个数或字母或者式子的正负，然后再求绝对值即可。
绝对值经典题目：
（1）当1<a<2时，代数式|a－2|＋|1－a|的值是（ ）
（2）表示实数a，b的点在数轴上的位置如图所示，化简
的结果是( )
（3）若|x|=7，|y|=5,那么|x-y|的值是
（4）实数a，b，c，d在数轴上的位置如图所示，下列关系式不正确的是（ ）
A．|a|＞|b| B．|ac|=ac C．b＜d D．c+d＞0
（5）若a≠0，b≠0，则代数式
的取值共有（ ）个
难点2 平方根，算术平方根
两者的区别：平方根有两个一正一负，这两个互为相反数；算术平方根只有一个正或0
联系：算术平方根是平方根正那个根，比如4的平方根是2或-2，算术平方根为2.
经典题目：
（1）
的算术平方根为（ ）（2）一个正数的平方根是x+1和x-5，则x=( )
(3)考察非负性。
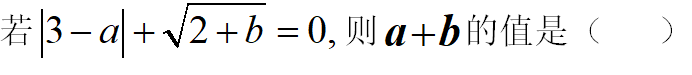
(4)已知a+1的算术平方根是1，﹣27的立方根是b﹣12，c﹣3的平方根是±2，求a+b+c的平方根．
