【九年级数学上】树状图法求概率问题

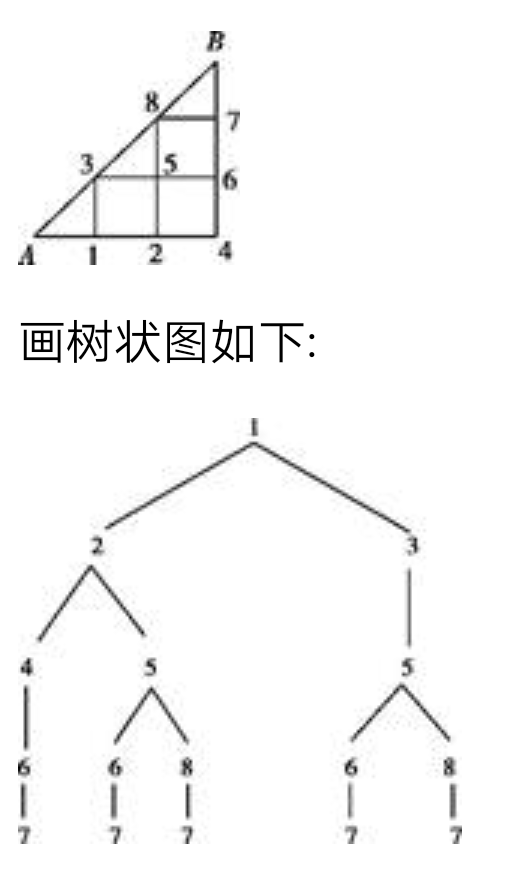
1. 树状图：层次感，结构感，步骤性

2. 树状图的步骤：

   （1）定：确定该试验的几个步骤、顺序、每一步可能产生的结果。

   （2）画：列举每一环节可能产生的结果，得到树状图。

   （3）数：数出全部均等的结果数m和该事件出现的结果数n。

   （4）算：代入公式P(A)=n÷m。

3. 适用范围：一次试验中要涉及两个及两个以上的因素，或随机事件的试验步骤有两步或两步以上，可以采用树状图列举求概率。

树状图解决两步概率问题

1.（山东泰安）袋中装有编号为1，2，3的三个质地均匀、大小相同的球，从中随机取出一球记下编号后，放入袋中搅匀，再从袋中随机取出一球，两次所取球的编号相同的概率为

A.9(1)                B.6(1)           C.3(1)               D.2(1)

解析：定：两个步骤，顺序：第一次，第二次，第一次取球有三种情况1,2,3，第二次由于先放回再取球也是三种情况1,2,3。

第一次取球                                     1                  2                      3

                                                  ╱∣╲              ∕∣╲                      ╱∣╲

第二次取球                              1  2    3       1   2   3              1   2    3        

P(两次编号相同）=31

2.（浙江温州）一个不透明的布袋里装有3个球，其中2个红球，1个白球，它们除颜色外其余都相同．

(1)求摸出1个球是白球的概率；

(2)摸出1个球，记下颜色后放回，并搅匀，再摸出1个球，求两次摸出的球恰好颜色不同的概率；摸出1个球，记下颜色后不放回，并搅匀，再摸出1个球，求两次摸出的球恰好颜色不同的概率。

解析：（1）直接求出即可，P（1球是白球）=31

 （2）①“放回” 

    第一步         红1                    红2                     白1

                ╱ ∣ ╲                ∕ ∣ ╲               ∕ ∣ ╲

   第二步     红1  红2  白1          红1  红2  白1           红1  红2  白1

P(两次颜色恰好不同）=4/9

②“不放回”

   第一步             红1                   红2                     白1

                    ╱  ╲                 ∕  ╲                  ∕  ╲                           

     第二步               红2     白1                     红1        白1                       红1     红2

P(两次颜色恰好不同）=2/6=1/3

注意：学会区分：“放回”和“不放回”。

3. （太原）小明和小亮转动转盘（每个转盘被分成四个面积相等的扇形）做游戏，转动两个转盘各一次，如次数字之和为奇数，则小明胜，否则小亮胜，这个游戏公平吗？

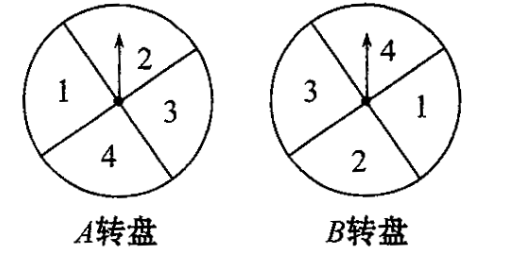
解析：公平性问题，实质就是算概率。     

          第一步              1                         2                             3                              4

                                ╱∣╲╲                  ╱∣╲╲                         ╱∣╲╲                         ╱∣╲╲ 

        第二步           1 2   3  4           1 2   3  4                   1 2   3  4                    1 2   3  4

P（奇数）=1/2            P(偶数）=1/2，故公平

4.(乌鲁木齐)在一个袋子中，有完全相同的4张卡片，把它们分别编号为1，2，3，4.

（1）从袋子中随机取两张卡片，求取出的卡片的编号之和等于4的概率；

（2）先从袋子中随机取一张卡片，记该卡片的编号为a，然后将其放回袋中，再从袋中随机取出一张卡片，记该卡片的编号为b，求满足a+2>b的概率.

5.如图所示电路图，有四个开关A,B,C,D和一个小灯泡，闭合开关D或同时闭合开关A,B,C都可使小灯泡发光，则任意闭合其中两个开关，小灯泡发光的概率是？

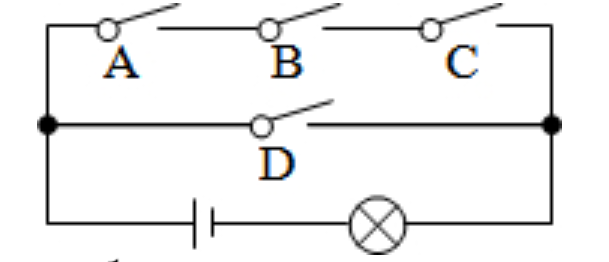
解析：任意闭合两个开关，分两步，第一步有4种情况（A,B,C,D）,第二步三种情况

   第一步      A                      B                   C                        D

                 ╱∣╲                   ∕∣╲                ╱∣╲                    ╱∣╲

  第二步   B  C  D             A  C D            A  B  D           A    B  C

小灯泡发光有6种情况，则P(发光概率）=6/12=1/2

树状图解决三步概率问题

1.（山东沂水）甲乙丙三人参加数学，物理，英语三项竞赛，每人限报一项，每项限报一人，则甲报英语，乙报数学，丙报物理的概率是？
解析：第一步甲                         数学                       物理                           英语

                                                ╱ ╲                          ╱ ╲                              ╱ ╲

         第二步乙                      物理  英语              数学 英语                       物理  数学

                                               ∣       ∣                    ∣       ∣                            ∣       ∣

         第三步丙                     英语     物理             英语     数学                   数学      物理

设甲报英语，乙报数学，丙报物理为事件A，则A共发生结果数为1，则P（A）=1/6.

2.春节期间小明进行填字游戏，将“新”，“年”，“好”三个字依次填写在三个空格中（每个空填一字，每空的字不重复）

，请用画树状图的方法求出小明排列顺序恰好是“新年好”的概率。

解析：三个空格，按照步骤从第一个空格填起，分三步。

      第一个空格                     新                                              年                                         好

                                          ╱ ╲                                              ╱ ╲                                       ╱ ╲ 

   第二个空格                   年   好                                            新  好                                  新  年

                                      ∣       ∣                                          ∣       ∣                                  ∣       ∣ 

   第三个空格                  好      年                                       好     新                                年       新

P（新年好）=1/6

3.（无锡中考）如图所示，是一个沿3×3正方形的对角线AB剪下的图形，一质点P由A点出发，沿格点线每次向右或向上运动1个单位长度，则点P由A点运动到B点的不同路径共有几条？

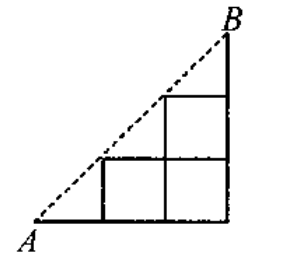
解析：