1. (山东枣庄)如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,且AC=CD,
∠ACD=120°.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.
解析:第(2)问
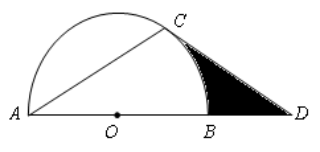
2. (山东东营)如图,已知点A、B、C、D 均在已知圆上,AD∥BC,BD平分∠ABC,∠BAD=120°,四边形ABCD的周长为15.
(1) 求此圆的半径;
(2) 求图中阴影部分的面积。 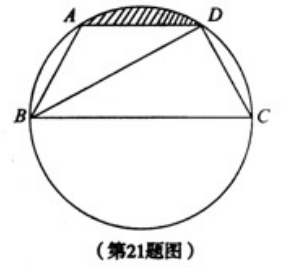
解析:第(1)问由AD∥BC,BD平分∠ABC,可得AD=AB,由∠BAD=120°,得∠ABD=∠DBC=30°,所以,AD=AB=DC,内接四边形对角互补,则∠C=60°,∠BDC=90°,得到BC是直径,且BC=2DC,5DC=15,DC=3,半径为3
第(2)问
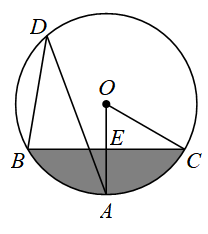
3.如图,在⊙O中,弦BC垂直于半径OA,垂足为E,D是优弧BC上一点,
连接BD,AD,OC,∠ ADB=30°.
(1)求∠AOC的度数;
(2)若弦BC=6cm,求图中阴影部分的面积.
4.直接组合
如下图,圆A、圆B、圆C、圆D、圆E相互外离,它们的半径都是1,顺次连结五个圆心得到五边形ABCDE,则图中五个扇形(阴影部分)的面积之和是( )
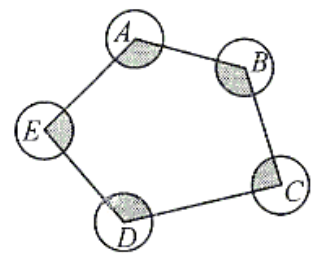
分析:由于每个扇形圆心角的具体角度未知,故无法直接进行计算。因为五边形ABCDE的内角和=540°=360°+180°,从而可知所求阴影部分的面积可以重新组合成一个圆和一个半圆的面积,即1.5个圆的面积:
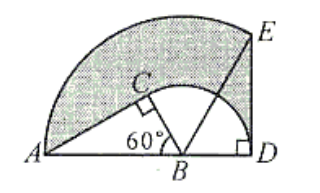
5.圆形分割
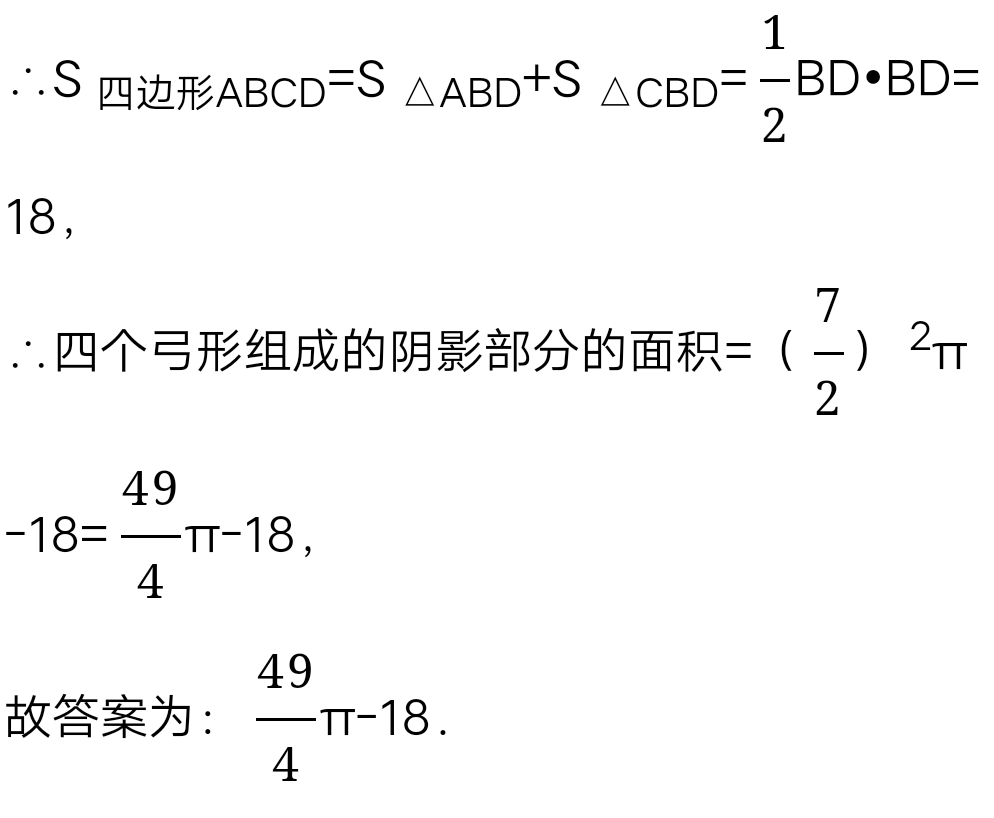
如下图,ΔABC中,∠C是直角,AB=12cm,∠ABC=60°,将ΔABC以点B为中心顺时针旋转,使点C旋转到AB边延长线上的点D处,则AC边扫过的图形(阴影部分)的面积是_________cm²(Π=3.14159……,最后结果保留三个有效数字)。

6.整体和差法
如下图,正方形的边长为a,以各边为直径在正方形内画半圆,所以围成的图形(阴影部分)的面积为______________。
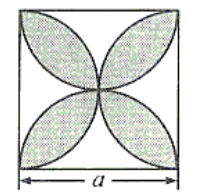
解:图中阴影部分面积可以看作是4个半圆的面积之和与正方形面积之差(重叠部分)
7.如图,四边形ABCD是⊙O的内接四边形,AC为直径,点B是弧AC的中点,若AC=7,BD=6,则阴影部分面积为?
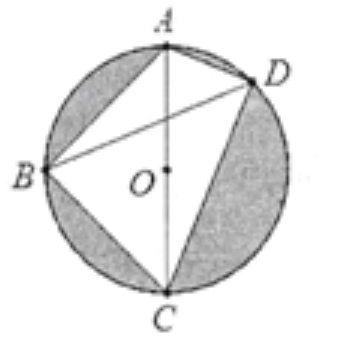
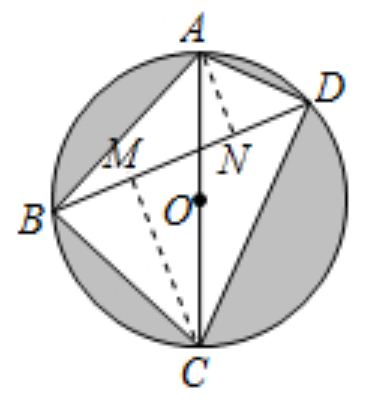
解析:过A作AN⊥BD于N,过C作CM⊥BD于M,可得