【九年上数学】关于圆的几个最小值问题

写在前面

关于圆的最小值问题，这里主要讲解简单的选择，填空问题。这类问题常与结合的知识点：动点问题，坐标系，勾股定理，两点之间线段最短，两边之和大于第三边，垂线段最短，三点共线······，主要用的数学思想：数形结合，数学转化。特别是转化思想，常把动点问题转化为定点，定长度问题，后列方程求解.

题目1

如图，⊙M的半径为2，圆心M坐标（3,4），点P是⊙M上的一动点，过点P作PA

⊥PB，A、B都在x轴上，且关于原点O对称，则AB最小值为多少？

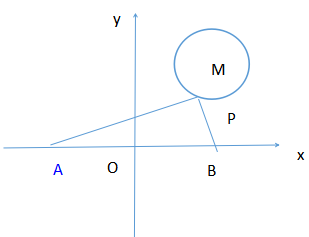
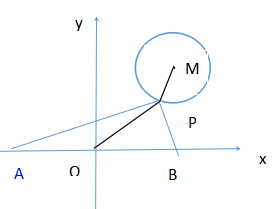
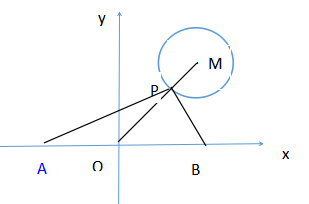
分析：由题目可知，三角形ABP是直角三角形，OP是斜边中线，只要知道OP最小，AB便最小（转化）。连接OP,PM，要使OP最小，只要使OP+PM最小即可。根据两点间线段最短或者两边之和大于第三边知O M最短进而本题得到解决.连接OM交圆于点P,由M(3,4),得出，OM=5，OP=3,则AB=6.

题目2

如图，在直角坐标系中，⊙A的圆心坐标为（-2,0），半径为2，点P为直线y=-3/4x+6上的动点，过点P作⊙A的切线，切点为Q，则切线长PQ的最小值是多少？

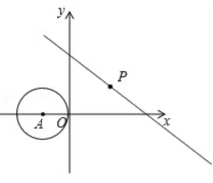
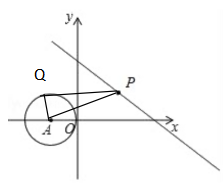
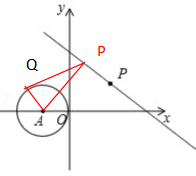
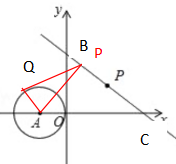
分析：如上第二图，任意作PQ相切⊙A，由勾股定理发现AQ²=AP²-PQ², 要求PQ最短只要AP最短即可，AP最短即从点A作直线的垂线段即可，如上第三个图，

接下来求PA,由△PAC≌△OBC，得PA=OB=6,所以可得AQ.

变式

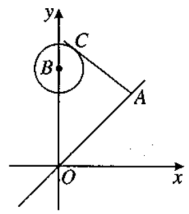
如图，在平面直角坐标系中，点A是直线y=x上移动点，以点B（0,4）为圆心，半径为1 的圆上有一点C，若直线AC与⊙B相切，切点为C，则线段AC的最小值是？

题目3

如图，Rt△ABC中，AB⊥BC,AB=6,BC=4.P是△ABC内部的一个动点，且满足∠PAB=∠PBC，则线段CP长最小值是多少？

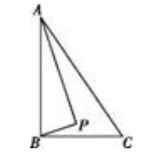
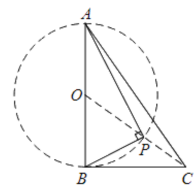
分析：由∠PAB=∠PBC，AB⊥BC，可得，∠P=90，想到P在以AB为直径的圆上运动，转化为O,P,C三点共线问题.

如上第二图，O,P,C三点共线。OC最短，即PC最小.

假设OC不最小，看下图

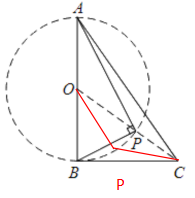
假设点P如图红色位置，连接OP,PC，由三角形三边之和大于第三边知，OP+PC>OC,故OC最短，有很多同学想不明白，让求PC最短为啥要看OC，因为OP是半径不变.

小结

这类题目在考试中，特别是初学者，满分率并不高。以上几个问题类型一致，方法，思想也都差不多.

要善于总结方法，发现相同类型题目，及时整理落到纸面上，以便养成简单逻辑思维和反思能力.