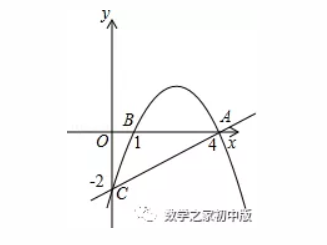
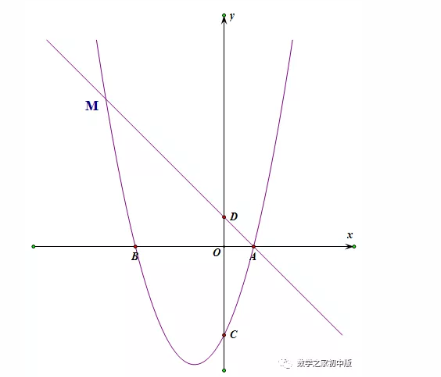
母题:如图,在平面直角坐标系中,点A、B在x轴上,点C、D在y轴上,且OB=OC=3,OA=OD=1,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点,直线AD与抛物线交于另一点M.
(1)求这条抛物线的解析式;
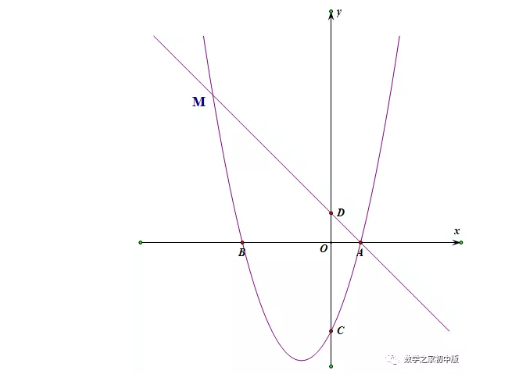
模型一
点P为抛物线上直线AM下方一动点,E为线段AM上一动点,且PE//Y轴,当点P的坐标为多少时,线段PE的长度有最大值?
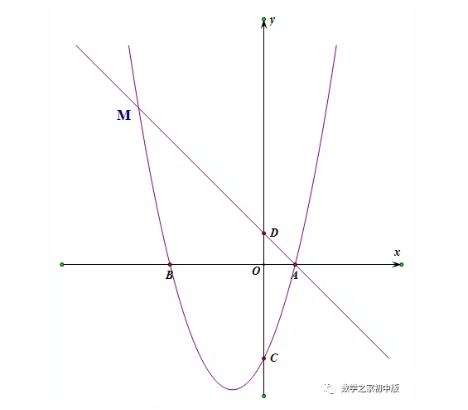
模型二
点P为抛物线上一动点,E为直线AM上一动点,是否存在点P,使以点D、C、E、P为顶点的四边形为平行四边形,若存在,请求出点P的横坐标,若不存在,请说明理由。
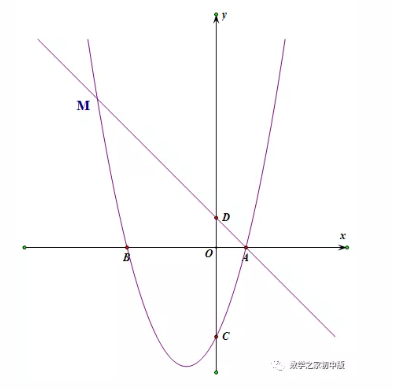
模型三
在抛物线的对称轴上是否存在点P,使得以点A、C、P为顶点的三角形为等腰三角形,若存在,请求出点P的坐标,若不存在,请说明理由。
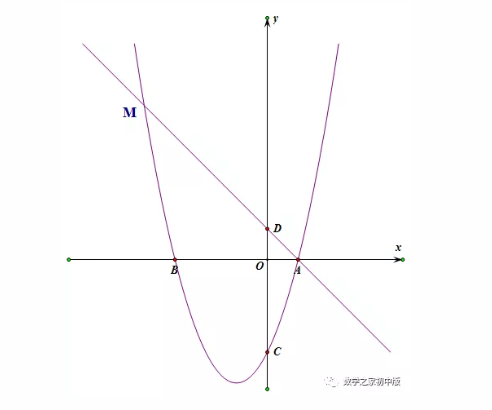
模型四
在抛物线的对称轴上是否存在一点P,使得△BMP是直角三角形,若存在,请求出点P的坐标,若不存在,请说明理由。
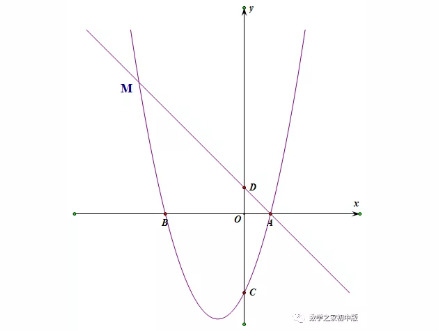
模型五
点P为抛物线上一动点,E为直线AD上一动点,是否存在点P,使以点A、P、E为顶点的三角形为等腰直角三角形?若存在,请求出所有点P的坐标;若不存在,请说明理由.
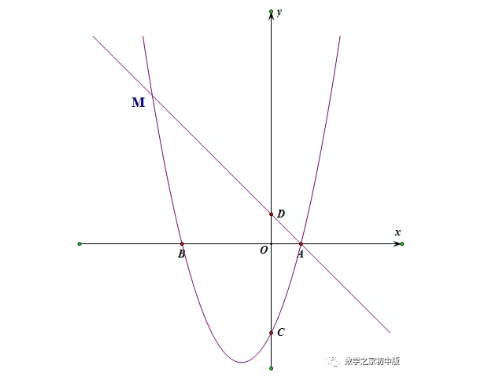
模型六
点P为抛物线上直线AM下方一动点,请求出△BMP面积的最大值。
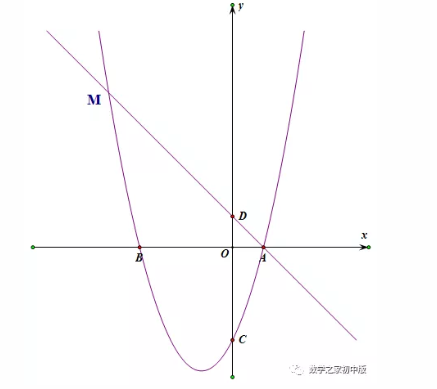
模型七
点P为X轴下方抛物线上一动点,当点P的坐标为多少时,四边形ACPB面积有最大值,并求出四边形ACPB面积的最大值.
模型八
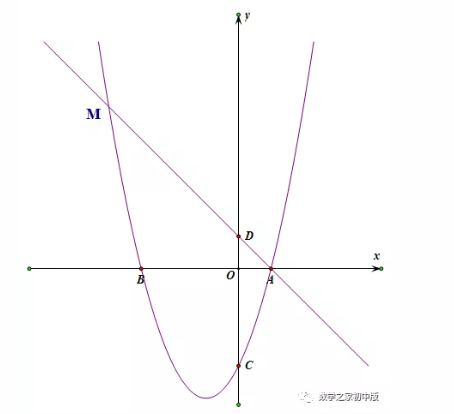
在抛物线对称轴上是否存在一点P,使得△BMP的周长最小,若存在,请求出点P的坐标,若不存在,请说明理由。
模型九
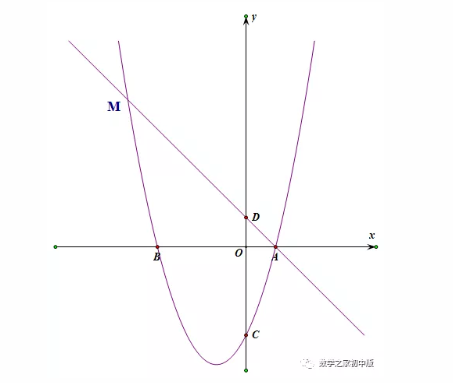
在抛物线的对称轴上找一点P,使得︳MP-BP︳的值最大,求出点P的坐标.
模型十
如图,抛物线经过A(4,0),B(1,0),C(0,﹣2)三点.
(1)求出抛物线的解析式;
(2)P是抛物线上一动点,过P作PM⊥ x轴,垂足为M,是否存在P点,使得以A,P,M为顶点的三角形与△ OAC相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;