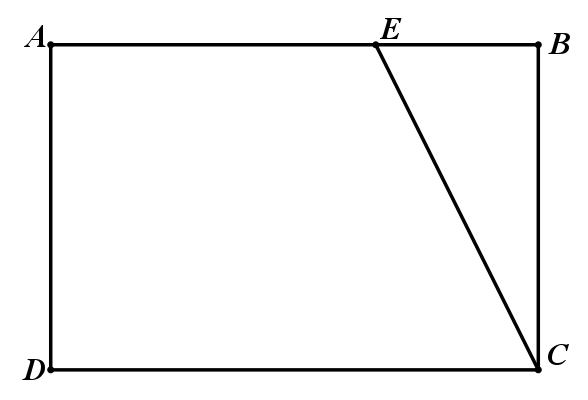
1. 如图,正方形ABCD的边长为7,以点B为圆心BA为半径画弧AC,点E在弧AC上,在线段BE上取一点F,使得BF=3,连接DE、CF,则CF+DE的最小值为
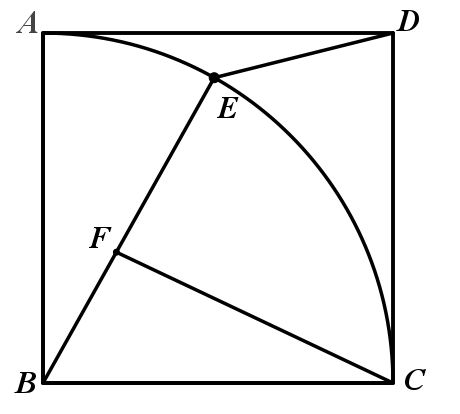
解:由于BE=BC=7,∠EBC=∠CBE,可构造对称全等。
截取BG=BF=3, 则△EBG≌△CBF , 则CF=BE

两动点转化为一动点:CF+DE=GE+DE,求BE+GE的最小值
两点之间线段最短:最小值即为GD=![]()
2. 如图点M是矩形ABCD内一个动点,AB=AM=6,BC=4,点N为线段AM上一点,且AN= ,连接BN
,连接BN
和CM,则 BN+CM的最小值为
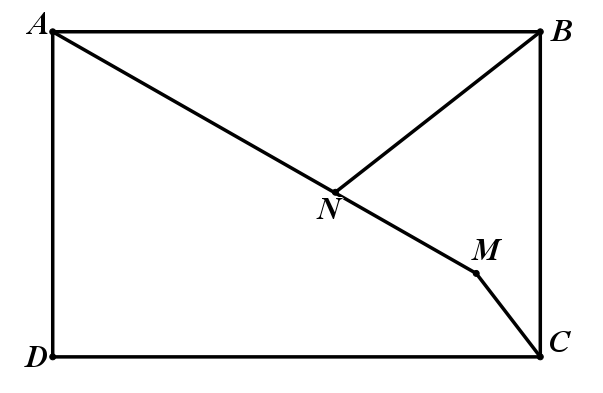
解:由于AB=AM=6,∠BAM=∠MAB,可构造对称全等。
截取AE=AN=4, 则△BAN≌△MAE , 则BN=EM
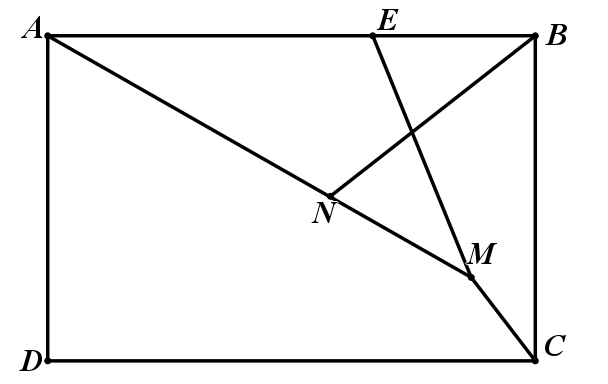
两动点转化为一动点:BN+CM=EM+CM,求EM+CM的最小值
两点之间线段最短:最小值即为EC=