一道好题DE的长为？，对称，隐圆，分类讨论

如图，在△ABC中，∠CAB=60°，∠B=75°，AB=4，AD平分∠CAB交BC于点D，在 AB边上存在一点E(不与点B重合),作△DBE 关于直线 DE的对称图形为△DFE,若点F落在△ABC的边上，则DE的长为？

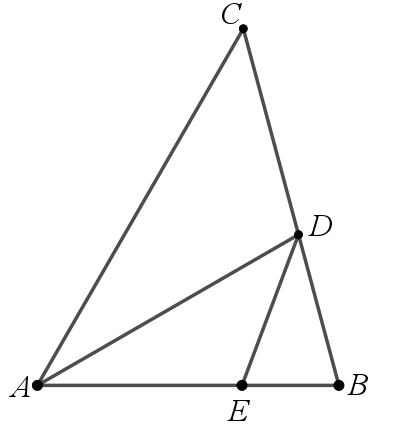
解析：因为点F与点B是对称点，由对称性知DB=DF，所以点F在以点D（定点）为圆心，半径为DB（定长）的圆上。

有以下四种情况，

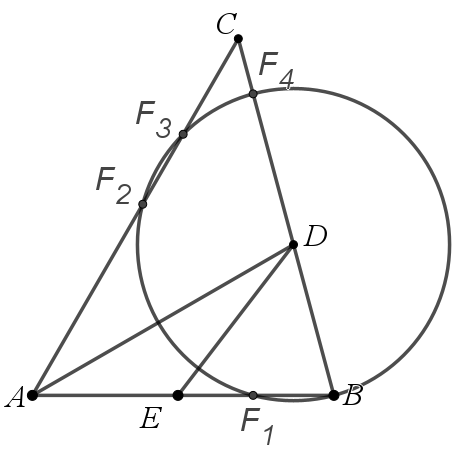
为什么圆会与AC相交有2个交点呢？这个问题一会回答。

当点在F₁ 时，DE⊥BF₁ ，BE=F₁E 。∠DAB=30°，

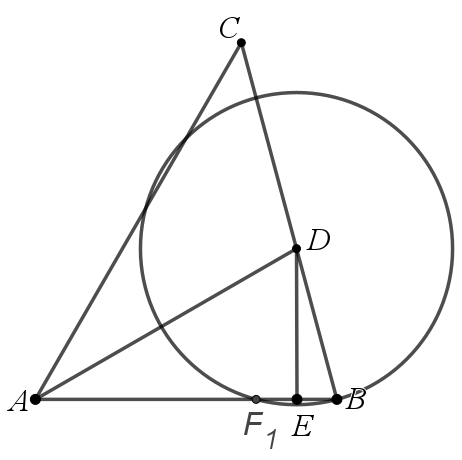
此时，由AD是∠BAC角平分线，角平分线性质得，DE=DE₁，DE=DE₁=2＜DB=DF，所以，圆会与AC相交有2个交点,如下图：

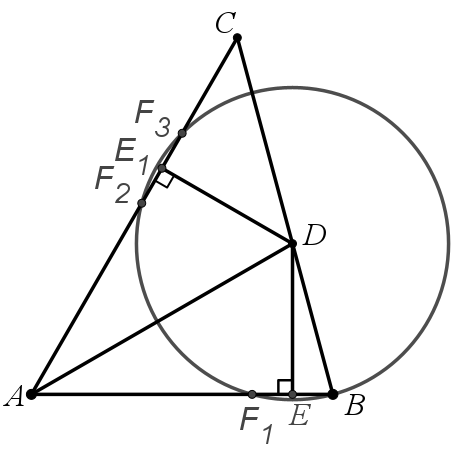
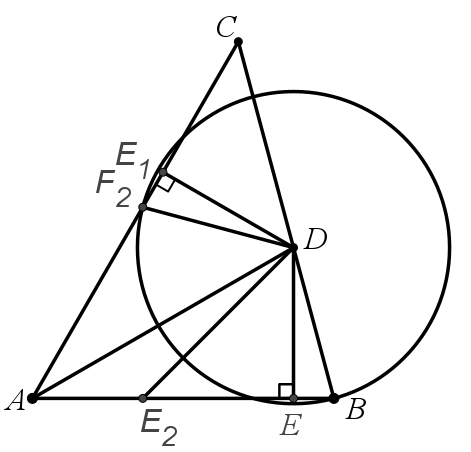
当点在F₂ 时，DE在DE₂如下图位置。可得，△AE₁D≌△AED, △F₂E₁D≌△BED

∠CAB=60° ,四边形ABDE₁中，∠BDE₁=120°，∠BDF₂=120°，则∠ADE=∠ADE₁=60°，

∠ADB=75°，∠F₂DE₁=∠BDE=15°，

由对称，∠F₂DE₂=∠BDE₂=60°，则，∠E₂DE=45°，△E₂DE₁为等腰直角三角形，

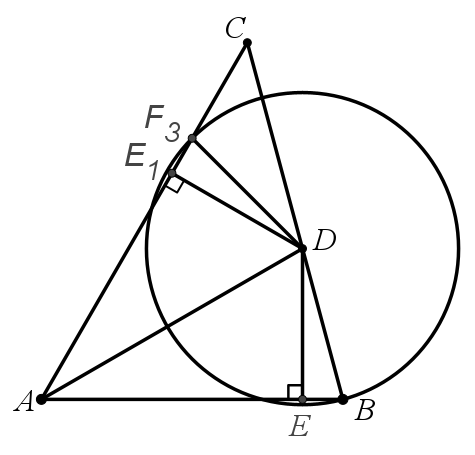
当点在F₃ 时, △AF₃D≌△ABD,点E与点A重合，ED=AD=4

当点在F₄ 时,点E不在AB上。

综上