题目
如图所示,已知抛物线交x轴与A,B两点。交y轴与C点,点A坐标(-1,0),OC=2,OB=3,D点为抛物线的顶点。
(1)求抛物线的解析式;
(2)P为坐标平面内一点,以B,C,D,P为顶点的四边形是平行四边形,求点P的坐标。
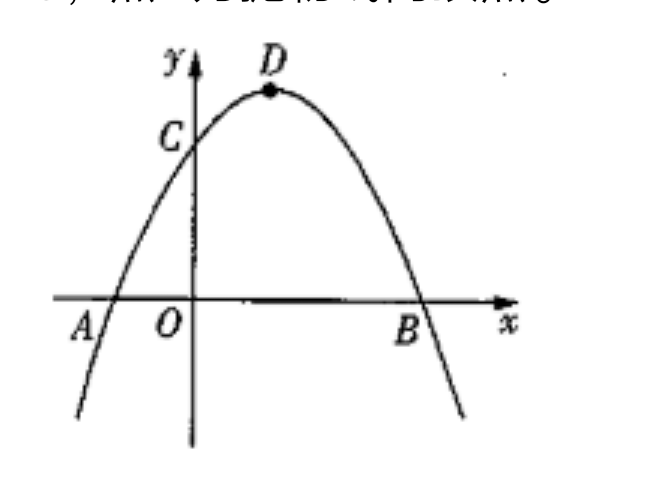
解析:第(1)问,可得A(-1,0),B(3,0),C(0,2)
方法一:设一般式y=ax2+bx+c,代入A,B,C三点坐标即可得
y=-2/3x2+4/3x+2
方法二、设交点式y=a(x-x1)(x-x2),交点A(-1,0),B(3,0)
解得,y=-2/3x2cx+2
第(2)问准备知识:
中点坐标公式:
若点A,B的坐标分别为(x₁,y₁),(x₂,y₂),则线段AB的中点C的坐标为.
(X,Y)=(x₁+x₂)/2,(y₁+y₂)/2,此公式为线段AB的中点坐标公式。
比如上图求AC中点坐标,A(-1,0),C(0,2),则AC中点坐标(-1/2,1)。
①当BC,DP为对角线。根据中点坐标公式,可得P(2,-3/2)
②当BD,CP为对角线。可得 P(4,2/3)
③当CD,PB为对角线,可得P(-2,14/3)
综上P(2,-3/2)或(4,2/3),(-2,14/3)
第(2)问视频讲解链接
练习
如图,抛物线y=1/2x2+x-3/2,与x轴相交于A,B两点,顶点为P
(1)求点A,B坐标
(2)在抛物线上是否存在点E,使△ABP的面积等于△ABE的面积?若存在,求出符合条件的点E的坐标;若不存在,请说明理由
(3)坐标平面内是否存在点F,使得以A、B、P、F为顶点的四边形为平行四边形?直接写所有符合条件的点F的坐标。
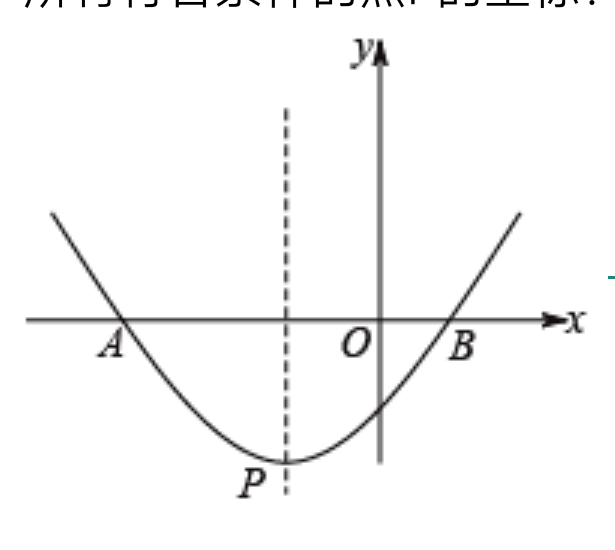
解析:(1)令y=0,可得A(-3,0),B(1,0)
(2)存在。抛物线对称轴,x=-1,得点P(-1,-2)
△ABP的面积等于△ABE的面积,点E到AB得距离是2,设点E(a,2)。
代入,抛物线解析式,得,a=-1-2√2或-1+2√2
E(-1-2√2,2)或(-1+2√2,2)。
(3) 如图 分别以AB,PA,PB为平行四边形的对角线确定平行四边形。
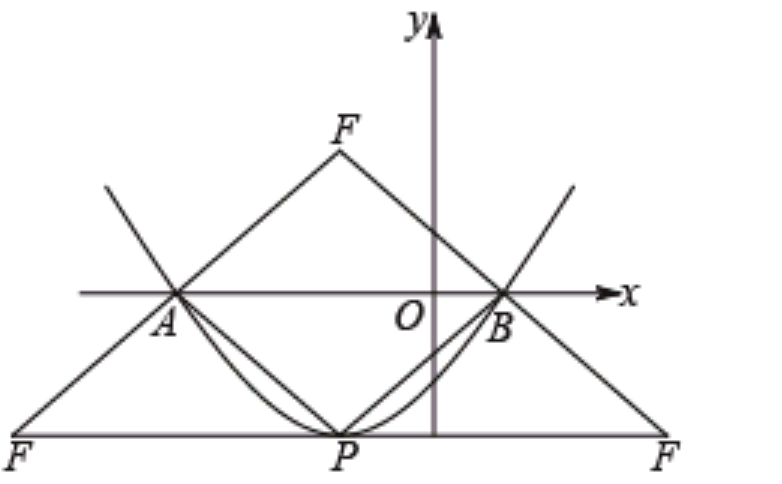
符合条件的点F(-1,2)、(3,-2)、(-5、-2)。
